Before we start, we have to know what is Galilean Relativity. You can check out this website: http://en.wikipedia.org/wiki/Galilean_invariance.
Frame A
A light beam is emitted from A to A', then back to B. Remember the light beam is travelling 90 degrees upward, A and B are basically the same point. The total time needed for the light beam to travel from A to B is given by:
Where c is the speed of light. However, the device moves at a speed v. Applying Galilean's Relativity to it, the frame below is formed.
Frame B
Instead of travelling up and down, the light beam travels in the track drew in red color above. However, to an observer moving along with the device, the light beam travels the same path as the beam traveled on frame A. The new distance traveled by the light beam is L. As the path was longer, the light beam will need a longer time to travel from A to B. The time needed is given by:
Applying the Pythagorean Theorem to the case, we get:
Since 2d/c is Δt0 in frame A, we obtain:
Upon rearranging, we find that:
This is the beautiful formula of Time Dilation. Perhaps you might notice that if we sub v=c (The device travels at the speed of light), we will get:
Humm, a division by zero error, not too good isn't?

.gif)

.gif)
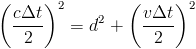
.gif)
.gif)
.gif)
.gif)
.gif)

No comments:
Post a Comment