After that much reading, it's time for some brain exercises.
Do you still remember the twin-brother, Obama and McCain? Okay, here's the story. When Obama was half way to Mars, he discovered that his greatest enemy, Bush, had installed a bomb in the spaceship. The bomb was programed to explode 1 year later. The only way to stop the bomb from exploding is to send it to the space station. The distance between the spaceship and the station is 1.3 light-year measured from the stationary space station. The max speed of which the space ship can travel is 80% speed of light. So can Obama get back on time and stop the bomb from exploding?
Click HERE for answers.
Friday, February 26, 2010
Proof(s) of Time Dilation
Perhaps most of you may think "You gotta be joking me" when you first read the Time Dilation theory. Time Dilation have already been proven. Below is the experiment used to prove Time Dilation. (You don't have to read if you believe in it XDD)
The first measurement of time dilation for radioactive particles moving at high speed relative to the earth was made in 1941 by Bruno Rossi and D.B. Hall. We will describe a similar measurement made in 1963 by D.H. Frisch and J.H. Smith(D.H.Frisch and J.H. Smith, "Measurement of Relativistic Time Dilation using μ-Mesons," American Journal of Physics, May 1963, p.342). The experiment involves the detection of muons, which are subatomic particles that are produced in the upper atmosphere and that rain down toward the earth with a speed close to the speed of light. As they Travel downward, some of them spontaneously decay in flight. Consequently, the number arriving at a medium altitude - say on top of a mountain - is greater than the number that survive to reach sea level. In their experiment, Frisch and Smith counted the number of muons having a narrow range of speeds near the peak of Mount Washington, New Hampshire. Then they went down to Cambridge, Massachusetts, and counted the muons that survived the trip down to sea level. The probability that a muon will decay, and thus its mean life, is determined only by forces within the muon itself. Therefore, any dependence of their mean life on their speed relative to us is due only to relativity.
Let's examine Frisch and Smith's findings in detail. The Mount Washington apparatus was set up to detect and stop muons with speed of 99.5% the speed of light. the time intervals between the arrival of a muon in the detecting apparatus and its subsequent decay were measured. Measurements from one run corresponded to a mean life of 2.2 μs. The average number of muons per hour arriving at this detector was 563. The time required for the muons to travel the 1907m from the elevation of the mountaintop to the elevation of the lab in Cambridge, measured with a clock stationary with respect to the lab, is:
After 6.4μs, only about 27 muons per hour would be expected to survive the trip down. But when detectors were set up in Cambridge to count muons of initial speed 0.995c, they observed an average rate of 408 muons per hour. We conclude that the muons decay more slowly when they are moving rapidly relative to us than when they are at rest relative to us.
How does the observed count of 408 muons per hour correspond to relativity predictions? According to our predictions, 408muons per hour correspond to an elapsed time of only 0.7μs. This means that time runs slower in the frame of reference of the moving muons than in the lab by a factor 0.7/6.4. We can check these results against the prediction of the Time Dilation formula by rearranging that equation for v and substituting for Δt0/Δt:
This calculated value for the speed of the muon in the lab frame is consistent with the value previously established for the experiment.
This experiment confirms time dilation and supports the special theory of relativity. Furthermore, it shows that relativistic effects can become large when the relative speed approach the speed of light. The effect observed here are general effects of relativity and are not limited to the special case of radioactive decay.
The first measurement of time dilation for radioactive particles moving at high speed relative to the earth was made in 1941 by Bruno Rossi and D.B. Hall. We will describe a similar measurement made in 1963 by D.H. Frisch and J.H. Smith(D.H.Frisch and J.H. Smith, "Measurement of Relativistic Time Dilation using μ-Mesons," American Journal of Physics, May 1963, p.342). The experiment involves the detection of muons, which are subatomic particles that are produced in the upper atmosphere and that rain down toward the earth with a speed close to the speed of light. As they Travel downward, some of them spontaneously decay in flight. Consequently, the number arriving at a medium altitude - say on top of a mountain - is greater than the number that survive to reach sea level. In their experiment, Frisch and Smith counted the number of muons having a narrow range of speeds near the peak of Mount Washington, New Hampshire. Then they went down to Cambridge, Massachusetts, and counted the muons that survived the trip down to sea level. The probability that a muon will decay, and thus its mean life, is determined only by forces within the muon itself. Therefore, any dependence of their mean life on their speed relative to us is due only to relativity.
Let's examine Frisch and Smith's findings in detail. The Mount Washington apparatus was set up to detect and stop muons with speed of 99.5% the speed of light. the time intervals between the arrival of a muon in the detecting apparatus and its subsequent decay were measured. Measurements from one run corresponded to a mean life of 2.2 μs. The average number of muons per hour arriving at this detector was 563. The time required for the muons to travel the 1907m from the elevation of the mountaintop to the elevation of the lab in Cambridge, measured with a clock stationary with respect to the lab, is:
How does the observed count of 408 muons per hour correspond to relativity predictions? According to our predictions, 408muons per hour correspond to an elapsed time of only 0.7μs. This means that time runs slower in the frame of reference of the moving muons than in the lab by a factor 0.7/6.4. We can check these results against the prediction of the Time Dilation formula by rearranging that equation for v and substituting for Δt0/Δt:
This experiment confirms time dilation and supports the special theory of relativity. Furthermore, it shows that relativistic effects can become large when the relative speed approach the speed of light. The effect observed here are general effects of relativity and are not limited to the special case of radioactive decay.
Dr. Edwin Jones and Dr. Richard Childers, "Relativity", Contemporary Collage Physics, 2001
Singularity of Special Relativity
In Einstein's Special Relativity, he stated that nothing can travel at or over the speed of light. According to his theory, all physics laws break down when something travels as fast as light or faster than it. In this post, I will explain why this happens.
It all happens in a factor called the Lorentz factor γ, that is:
Like I said before, if we sub v=c into the γ, we get a division by zero error. Just like Time Dilation, if we sub v=c into that formula, time expands unlimitedly. If we sub v=c into the formulae of Special Relativity, we get unreasonable values. For example, Length Contraction, Relativistic Momentum, Relativistic Kinetic Energy, Relativistic Doppler Effect, etc. Here are the Calculation steps.
Length Contraction:
According to Einstein's theory, if something travels at the speed of light, to an observer on that thing, length of everything shall reduce to 0.
Relativistic Momentum:
According to Einstein's theory, if something travels at the speed of light, it carries unlimited amount of momentum.
Relativistic Kinetic Energy:
It all happens in a factor called the Lorentz factor γ, that is:
Like I said before, if we sub v=c into the γ, we get a division by zero error. Just like Time Dilation, if we sub v=c into that formula, time expands unlimitedly. If we sub v=c into the formulae of Special Relativity, we get unreasonable values. For example, Length Contraction, Relativistic Momentum, Relativistic Kinetic Energy, Relativistic Doppler Effect, etc. Here are the Calculation steps.
Length Contraction:
Relativistic Momentum:
Relativistic Kinetic Energy:
According to Einstein's theory, if something travels at the speed of light, it carries unlimited amount of kinetic energy.
In these conditions, normal physics laws break down. No one knows what happens when something travels at the speed of light. It is a singularity of Special Relativity. Therefore, Einstein stated that nothing can travel faster than light.
Division by Zero (Part III)
In my last post, I used the Time Dilation to prove the division by zero. However, some of the people who read my blog told me that they still don't really understand the proof. So, in this post, I will explain the theory again.
Firstly, what is Galilean Relativity? Take a look at the graph below.
In the graph, observer A in (a) is in a moving vehicle and is throwing a ball upward. The path in (a) is observed by observer A. However, to a stationary observer (observer B), the path observed is the path in (b). Einstein applied this theory to the light beam in Time Dilation. The frame A below is (a) in the above graph while B is (b) in the graph.
Frame A Frame B
Now we have a clearer image on Galilean Relativity, we can understand the Time Dilation of Special Relativity easier. I hope you still remember the formula of Time Dilation.Now, sub v=c into the formula, we get:
We had discussed about the division by zero error before. Bhaskara Achārya defined that n/0 = .gif) . So, how did time go infinite? Take a look at the picture below.
. So, how did time go infinite? Take a look at the picture below.
.gif) . So, how did time go infinite? Take a look at the picture below.
. So, how did time go infinite? Take a look at the picture below.In the picture,
θ is the angle between the ground and the path of which the light beam travels. The relationship between
θ and the velocity is as below:
Let's suppose the height of the device is 1m, the proper time is 1s and it travels at the speed of light. Sub those information into the formula of Time Dilation, we get:
Since v=c,
So, the angle between the path and the ground is 0. So, the light beam will never meet A', or we can say that it will take 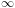.gif) time to travel from A to A', then to B. That's why n/0 is equal to
time to travel from A to A', then to B. That's why n/0 is equal to
.gif) time to travel from A to A', then to B. That's why n/0 is equal to
time to travel from A to A', then to B. That's why n/0 is equal toTuesday, February 23, 2010
Division by Zero (Part II)
To understand how the error occurred, we first have to understand the changes on the path of which light travels when the speed varies. Below shows a frame.
Frame A
In the frame, the red path shows the path of which the light beam travels when the device moves at the speed v. When the speed increases to v', instead of travelling through the red path, it travels through the orange path. The angle between the path and the ground reduces when the speed increases. So, if the device travels at 99% the speed of light, the angle between the path and the ground will be very close to zero, similar to the frame below.
When the speed reaches the speed of light, the angle will become 0 degree. The light beam could never meet A'. The light beam will take .gif) time to travel A to A'. In other words, to an observer travelling along with the device at the speed of light, time stops. This proves that
time to travel A to A'. In other words, to an observer travelling along with the device at the speed of light, time stops. This proves that
.gif) time to travel A to A'. In other words, to an observer travelling along with the device at the speed of light, time stops. This proves that
time to travel A to A'. In other words, to an observer travelling along with the device at the speed of light, time stops. This proves that is correct.
Division by Zero (Part I)
Last time we obtain a Division by Zero error, so today we are going to learn more about it and explain why we get a division by zero error in the formula.
"In mathematics, a division is called a division by zero if the divisor is zero. Such a division can be formally expressed as n/0 where a is the dividend. Whether this expression can be assigned a well-defined value depends upon the mathematical setting. In ordinary (real number) arithmetic, the expression has no meaning."
Division by Zero from Wikipedia, the free encyclopedia.
As wiki said, Division by Zero means a division with a divisor of zero. Bhaskara Achārya tried to solve the problem by defining (in modern notation):
This makes some sense. You can check out this website if you want to know how it's proved.
Division by zero error can cause serious accidents. For example, On September 21, 1997, a divide by zero error on board the USS Yorktown (CG-48). Remote Data Base Manager brought down all the machines on the network, causing the ship's propulsion system to fail.
So, how did Division by Zero error occur in the formula??
Einstein's Time Dilation (Part II)
Now that you have the basic concept of Time Dilation, let's go a little deeper. In this post, I am going to introduce the time dilation to you in Mathematics. The time dilation formula is closely related to the Pythagorean Theorem. Without the Pyth Thm, Einstein would not be able to give us the amazing formula of time dilation.
Before we start, we have to know what is Galilean Relativity. You can check out this website: http://en.wikipedia.org/wiki/Galilean_invariance.
We can derive the mathematical expression of Time Dilation from the following thought experiment. The frame below shows a device.
Before we start, we have to know what is Galilean Relativity. You can check out this website: http://en.wikipedia.org/wiki/Galilean_invariance.
Frame A
A light beam is emitted from A to A', then back to B. Remember the light beam is travelling 90 degrees upward, A and B are basically the same point. The total time needed for the light beam to travel from A to B is given by:
Where c is the speed of light. However, the device moves at a speed v. Applying Galilean's Relativity to it, the frame below is formed.
Frame B
Instead of travelling up and down, the light beam travels in the track drew in red color above. However, to an observer moving along with the device, the light beam travels the same path as the beam traveled on frame A. The new distance traveled by the light beam is L. As the path was longer, the light beam will need a longer time to travel from A to B. The time needed is given by:
Applying the Pythagorean Theorem to the case, we get:
Since 2d/c is Δt0 in frame A, we obtain:
Upon rearranging, we find that:
This is the beautiful formula of Time Dilation. Perhaps you might notice that if we sub v=c (The device travels at the speed of light), we will get:
Humm, a division by zero error, not too good isn't?
Monday, February 22, 2010
Einstein's Time Dilation (Part I)
In 1905, Einstein published the special relativity. This theory of relativity challenged the Newtonian view and has affected the way people look at the world. The theory states the most physics laws cannot be used in an object approaching the speed of light. The theory stated some intriguing phenomenon, like Time Dilation, Length Contraction, Mass-Energy Relation, etc. The most intriguing phenomenon of all is the phenomenon of time dilation.
Now, to have a basic concept of Time Dilation, I have made it into a story.
Once upon a time, there were a pair of twins at the same age. One was called Obama, and the other was called McCain. Obama was an astronaut and McCain was a scientist. One day, Obama went on a trip to Mars. He traveled on a space ship travelling at 80% the speed of light. 5 years later, he returned. However, when he came back, he found that McCain was a lot older than he was. How did that happen?!
In this case, Time Dilation occurred.
Long ago, Newton stated that time is like a straight line, separated from space.
Proofs of Pythagorean Theorem
Proof #1
Now take a good look at the picture below.
The picture above shows 4 identical right-triangle. Each of them has an area of A. Area A is given by:
Now, if we put the four triangle together to form the square below:
Now take a good look at the picture below.
The picture above shows 4 identical right-triangle. Each of them has an area of A. Area A is given by:
Now, if we put the four triangle together to form the square below:
The square above has a hole inside it. The total area of the square is given by:
Proof #2
The polygon below is a trapezoid.
The area of the trapezoid is given by:
The area of the trapezoid can also be calculated in:
There are lots of proofs for Pyth Thm. The above are just the two of them. The Pyth Thm is so useful that even Einstein uses it in his calculations on Time Dilation in Special Relativity. On my next post, I will give an introduction on Time Dilation.
Subscribe to:
Comments (Atom)


.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)



.gif)
.gif)

.gif)
.gif)
.gif)
.gif)
.gif)

.gif)
.gif)

.gif)

.gif)
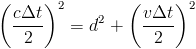
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)

.gif)

.gif)
.gif)
.gif)

.gif)
.gif)
.gif)
.gif)
