 In the days before, we had discussed about the relationships between Pythagorean Theorem and the Special Relativity. But today I am not gonna talk about the Pythagorean Theorem. Instead, I will talk about something more interesting, the Mass-Energy Relation of Special Relativity.
In the days before, we had discussed about the relationships between Pythagorean Theorem and the Special Relativity. But today I am not gonna talk about the Pythagorean Theorem. Instead, I will talk about something more interesting, the Mass-Energy Relation of Special Relativity.
The most dramatic example of energy released by a change in an object's mass is the release of energy in nuclear reactions, especially in fission and fusion. So, how did Einstein came up with his "God Formula" ? First, we have to understand that light carries momentum.
In Maxwell's electromagnetic theory, a prediction was made. The theory stated that when light strikes an object, it exerts a pressure. The presence of this pressure implies that light waves carry momentum. Moreover, the theory requires that this momentum be proportional to the energy carried by the light wave. With experiments supporting the theory, the result is that a wave carrying an amount of energy E has a momentum given by:
where c is the speed of light and p is the momentum carried by the light wave. We shall use this result and the principle of conservation of momentum to derive a relation between mass and energy.
Let's consider a thought experiment given by Einstein. Take a look at the frame below.
There are two frames above us. At t=0, the box is at rest and emitted a light beam (orange). Remember that the box is suspended so that it's free to move without friction. According to the conservation of momentum, the box must recoil with an equal but opposite momentum, of magnitude:
Where v is the recoil velocity of the box and E is the energy carried by the light beam.
The light beam requires a time t to reach the other end of the box, where it's completely absorbed. During the time L/c, the box moves a distance x as it recoils. When the light beam is absorbed at the other end, the box stops and return to rest, in agreement of conservation of momentum.
Since no outside forces act on the box, its center mass must not move during this event, even though the position of the box obviously changes. The only way this can happen is for a shift of mass to occur within the box as it moves, maintaining the position of the center mass. Consequently, there must be an equivalent mass m associated with the light, of such magnitude that while the box of mass M moves a distance -x, it's movement about the center mass is compensated by the light moving a distance L:
Since we know the momentum of the box, and thus its velocity, we can use this information along with the time of flight of the light to evaluate the distance x that the box moves by the multiplying the speed v to give
The elapsed time t is the time it takes for the light to travel the distance L. Thus, we have:
Using this value for x and solving for the energy E, we get:
This is Einstein's Mass-Energy Relation.

.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)



.gif)
.png)

.gif)


.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)


.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)



.gif)
.gif)
.gif)

.gif)
.gif)
.gif)
.gif)
.gif)
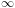.gif)
